
 PhD student in Applied Mathematics and Computational Sciences (AMCS) at KAUST
PhD student in Applied Mathematics and Computational Sciences (AMCS) at KAUSTUNDER CONSTRUCTION!
Hello, fellow web browsing-capable beings! I am an Ecuadorian applied mathematician working on numerical methods for partial differential equations (PDEs). I am interested in hyperbolic, nonlinear, and dispersive PDEs and their applications in fluid dynamics, in particular water waves and tsunami modeling. I am currently a PhD student in the Numerical Mathematics Group at KAUST, under supervision of Prof. David Ketcheson.
Warning
Problem: The current name of your GitHub Pages repository ("Solution: Please consider renaming the repository to "
http://".
However, if the current repository name is intended, you can ignore this message by removing "{% include widgets/debug_repo_name.html %}" in index.html.
Action required
Problem: The current root path of this site is "baseurl ("_config.yml.
Solution: Please set the
baseurl in _config.yml to "Education
-
 King Abdullah University of Science and Technology (KAUST), Saudi ArabiaComputer, Electrical and Mathematical Sciences and Engineering Division (CEMSE)
King Abdullah University of Science and Technology (KAUST), Saudi ArabiaComputer, Electrical and Mathematical Sciences and Engineering Division (CEMSE)
Ph.D. Student in Applied Mathematics and Computational Sciences2022 - present -
 King Abdullah University of Science and Technology (KAUST), Saudi ArabiaM.S. in Applied Mathematics and Computational Sciences2021 - 2022
King Abdullah University of Science and Technology (KAUST), Saudi ArabiaM.S. in Applied Mathematics and Computational Sciences2021 - 2022 -
 Yachay Tech University, EcuadorB.S. in Mathematics (under Prof. Juan Mayorga-Zambrano)2015 - 2020
Yachay Tech University, EcuadorB.S. in Mathematics (under Prof. Juan Mayorga-Zambrano)2015 - 2020
Honors & Awards
-
Dean's list in the Applied Mathematics and Computational Science program, KAUST2024
-
Graduated Cum Laude, Yachay Tech2020
-
Academic excellence scholarship, Yachay Tech2016
News
Selected Publications (view all )
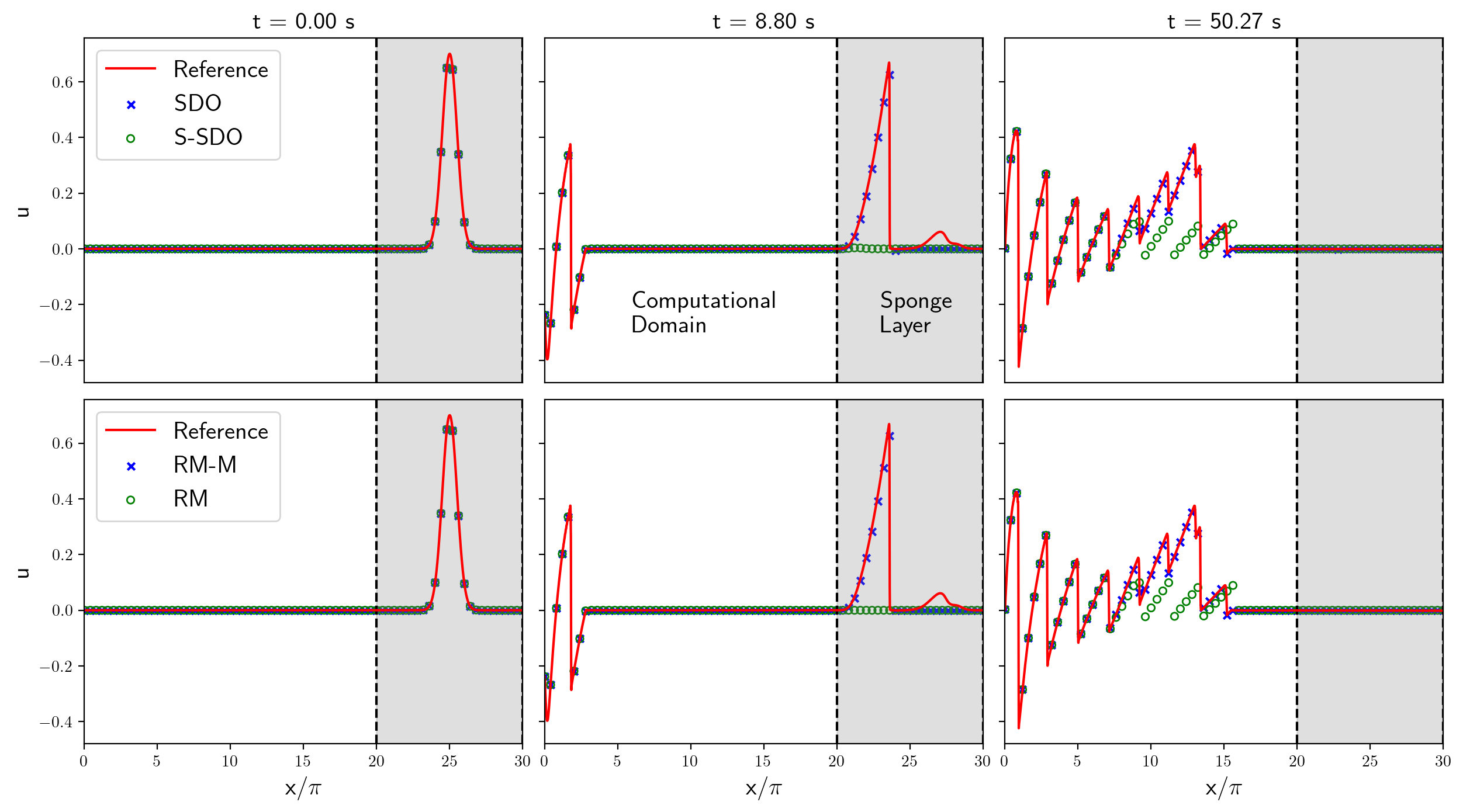
A Unified Framework for Sponge-Layer Relaxation Methods and Damping Operators for Conservation Laws: Application to the Piston Problem of Gas Dynamics
Carlos Muñoz-Moncayo
Journal of Engineering Mathematics (To appear)
This work addresses the imposition of outflow boundary conditions for one-dimensional conservation laws. While a highly accurate numerical solution can be obtained in the interior of the domain, boundary discretization can lead to unphysical reflections. We investigate and implement some classes of relaxation methods and far-field operators to deal with this problem without significantly increasing the size of the computational domain. We formulate these methods within a framework that allows to reveal relationships among them, and to propose novel extensions. In particular, we introduce a simple and robust relaxation method with a matrix-valued weight function that selectively absorbs outgoing waves. As a challenging model problem, we consider the Lagrangian formulation of the Euler equations for a polytropic gas with inflow boundary conditions determined by an oscillating piston.
A Unified Framework for Sponge-Layer Relaxation Methods and Damping Operators for Conservation Laws: Application to the Piston Problem of Gas Dynamics
Carlos Muñoz-Moncayo
Journal of Engineering Mathematics (To appear)
This work addresses the imposition of outflow boundary conditions for one-dimensional conservation laws. While a highly accurate numerical solution can be obtained in the interior of the domain, boundary discretization can lead to unphysical reflections. We investigate and implement some classes of relaxation methods and far-field operators to deal with this problem without significantly increasing the size of the computational domain. We formulate these methods within a framework that allows to reveal relationships among them, and to propose novel extensions. In particular, we introduce a simple and robust relaxation method with a matrix-valued weight function that selectively absorbs outgoing waves. As a challenging model problem, we consider the Lagrangian formulation of the Euler equations for a polytropic gas with inflow boundary conditions determined by an oscillating piston.
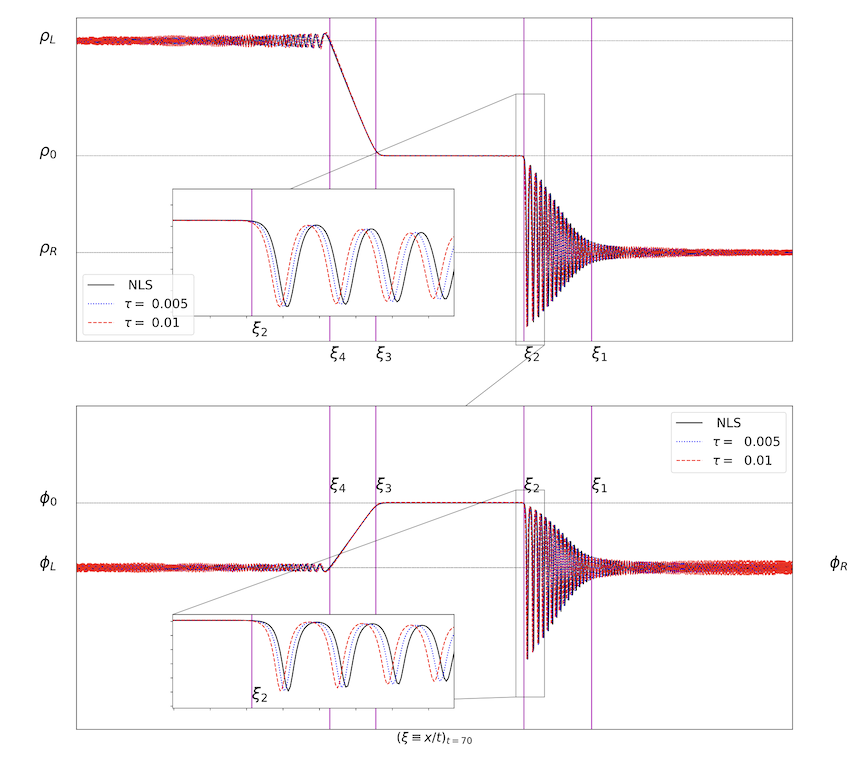
A Hyperbolic Approximation of the Nonlinear Schrödinger Equation
Abhijit Biswas, Laila S. Busaleh, David I. Ketcheson, Carlos Muñoz-Moncayo, Manvendra Rajvanshi
Studies in Applied Mathematics 2025
We study a first-order hyperbolic approximation of the nonlinear Schr\"odinger (NLS) equation. We show that the system is strictly hyperbolic and possesses a modified Hamiltonian structure, along with at least three conserved quantities that approximate those of NLS. We provide families of explicit standing-wave solutions to the hyperbolic system, which are shown to converge uniformly to ground-state solutions of NLS in the relaxation limit. The system is formally equivalent to NLS in the relaxation limit, and we develop asymptotic preserving discretizations that tend to a consistent discretization of NLS in that limit, while also conserving mass. Examples for both the focusing and defocusing regimes demonstrate that the numerical discretization provides an accurate approximation of the NLS solution.
A Hyperbolic Approximation of the Nonlinear Schrödinger Equation
Abhijit Biswas, Laila S. Busaleh, David I. Ketcheson, Carlos Muñoz-Moncayo, Manvendra Rajvanshi
Studies in Applied Mathematics 2025
We study a first-order hyperbolic approximation of the nonlinear Schr\"odinger (NLS) equation. We show that the system is strictly hyperbolic and possesses a modified Hamiltonian structure, along with at least three conserved quantities that approximate those of NLS. We provide families of explicit standing-wave solutions to the hyperbolic system, which are shown to converge uniformly to ground-state solutions of NLS in the relaxation limit. The system is formally equivalent to NLS in the relaxation limit, and we develop asymptotic preserving discretizations that tend to a consistent discretization of NLS in that limit, while also conserving mass. Examples for both the focusing and defocusing regimes demonstrate that the numerical discretization provides an accurate approximation of the NLS solution.

Asymptotic Behaviour of Infinitely Many Solutions for the Finite Case of a Nonlinear Schrödinger Equation with Critical Frequency
Juan Mayorga-Zambrano#, Leonardo Medina-Espinosa, Carlos Muñoz-Moncayo (# corresponding author)
Differential Equations and Dynamical Systems 2023
We consider an N-dimensional nonlinear Schrödinger equation $(P_{\varepsilon})$ with a positive Planck constant $\varepsilon>0$ and power nonlinearity $p>1$. We consider the finite case and critical frequency as described by Byeon and Wang, i.e., the continuous non-negative potential's zero level set is a singleton, around which it decays like a homogeneous positive function. In the limit $\varepsilon \to 0$, we denote the semiclassical limit problem by $(P_{\text{lim}})$. By a Ljusternik-Schnirelman scheme we get an infinite number of solutions for $(P_{\varepsilon})$ and $(P_{\text{lim}})$, $v_{k,\varepsilon}$ and $w_k$, respectively. We prove, up to a scaling, that (a) $v_{k,\varepsilon}$ subconverges to $w_k$ pointwise and in Sobolev-like norm, (b) the energy of $v_{k,\varepsilon}$ converges to that of $w_k$, and (c) $v_{k,\varepsilon}$ exponentially decays out of the zero level set of the potential.
Asymptotic Behaviour of Infinitely Many Solutions for the Finite Case of a Nonlinear Schrödinger Equation with Critical Frequency
Juan Mayorga-Zambrano#, Leonardo Medina-Espinosa, Carlos Muñoz-Moncayo (# corresponding author)
Differential Equations and Dynamical Systems 2023
We consider an N-dimensional nonlinear Schrödinger equation $(P_{\varepsilon})$ with a positive Planck constant $\varepsilon>0$ and power nonlinearity $p>1$. We consider the finite case and critical frequency as described by Byeon and Wang, i.e., the continuous non-negative potential's zero level set is a singleton, around which it decays like a homogeneous positive function. In the limit $\varepsilon \to 0$, we denote the semiclassical limit problem by $(P_{\text{lim}})$. By a Ljusternik-Schnirelman scheme we get an infinite number of solutions for $(P_{\varepsilon})$ and $(P_{\text{lim}})$, $v_{k,\varepsilon}$ and $w_k$, respectively. We prove, up to a scaling, that (a) $v_{k,\varepsilon}$ subconverges to $w_k$ pointwise and in Sobolev-like norm, (b) the energy of $v_{k,\varepsilon}$ converges to that of $w_k$, and (c) $v_{k,\varepsilon}$ exponentially decays out of the zero level set of the potential.