2026
Adaptive, efficient, and scalable water wave modeling with dispersive hyperbolic systems
Carlos Muñoz-Moncayo, David I. Ketcheson
arXiv preprint 2026-06-10
Accurate modeling of tsunamis (such as those generated by landslides) requires capturing both wave dispersion in the deep ocean and wave breaking near the shore. The shallow water equations are often preferred for working with tsunamis, but neglect dispersion and may be inaccurate in scenarios where dispersive effects are significant. In this work, we develop an approach that seeks to incorporate the best aspects of both hyperbolic and dispersive models by combining either of two hyperbolic reformulations of the Serre-Green-Naghdi equations away from the shore with the non-dispersive shallow water equations near the shore. The model is discretized and implemented within the GeoClaw software, and incorporates adaptive mesh refinement as well as shared-memory parallelism. We validate it through comparison with benchmarks and real tsunami data. The results and performance compare favorably with the existing dispersive water wave solvers, including a speedup of about 2x relative to GeoClaw's existing dispersive solver for a large-scale tsunami simulation.
Adaptive, efficient, and scalable water wave modeling with dispersive hyperbolic systems
Carlos Muñoz-Moncayo, David I. Ketcheson
arXiv preprint 2026-06-10
Accurate modeling of tsunamis (such as those generated by landslides) requires capturing both wave dispersion in the deep ocean and wave breaking near the shore. The shallow water equations are often preferred for working with tsunamis, but neglect dispersion and may be inaccurate in scenarios where dispersive effects are significant. In this work, we develop an approach that seeks to incorporate the best aspects of both hyperbolic and dispersive models by combining either of two hyperbolic reformulations of the Serre-Green-Naghdi equations away from the shore with the non-dispersive shallow water equations near the shore. The model is discretized and implemented within the GeoClaw software, and incorporates adaptive mesh refinement as well as shared-memory parallelism. We validate it through comparison with benchmarks and real tsunami data. The results and performance compare favorably with the existing dispersive water wave solvers, including a speedup of about 2x relative to GeoClaw's existing dispersive solver for a large-scale tsunami simulation.
2025
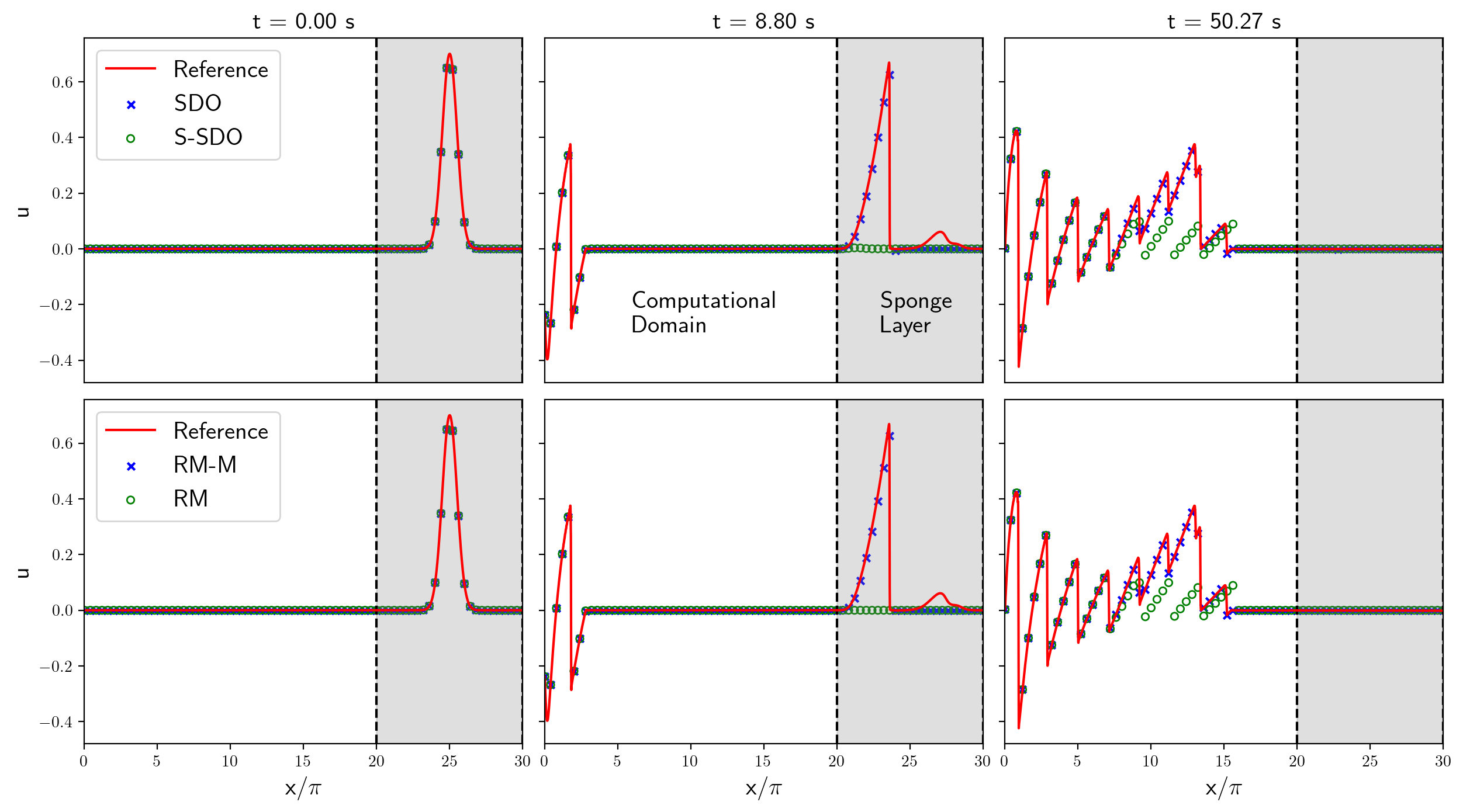
A Unified Framework for Sponge-Layer Relaxation Methods and Damping Operators for Conservation Laws: Application to the Piston Problem of Gas Dynamics
Carlos Muñoz-Moncayo
Journal of Engineering Mathematics 2025-12-15
This work addresses the imposition of outflow boundary conditions for one-dimensional conservation laws. While a highly accurate numerical solution can be obtained in the interior of the domain, boundary discretization can lead to unphysical reflections. We investigate and implement some classes of relaxation methods and far-field operators to deal with this problem without significantly increasing the size of the computational domain. We formulate these methods within a framework that allows to reveal relationships among them, and to propose novel extensions. In particular, we introduce a simple and robust relaxation method with a matrix-valued weight function that selectively absorbs outgoing waves. As a challenging model problem, we consider the Lagrangian formulation of the Euler equations for a polytropic gas with inflow boundary conditions determined by an oscillating piston.
A Unified Framework for Sponge-Layer Relaxation Methods and Damping Operators for Conservation Laws: Application to the Piston Problem of Gas Dynamics
Carlos Muñoz-Moncayo
Journal of Engineering Mathematics 2025-12-15
This work addresses the imposition of outflow boundary conditions for one-dimensional conservation laws. While a highly accurate numerical solution can be obtained in the interior of the domain, boundary discretization can lead to unphysical reflections. We investigate and implement some classes of relaxation methods and far-field operators to deal with this problem without significantly increasing the size of the computational domain. We formulate these methods within a framework that allows to reveal relationships among them, and to propose novel extensions. In particular, we introduce a simple and robust relaxation method with a matrix-valued weight function that selectively absorbs outgoing waves. As a challenging model problem, we consider the Lagrangian formulation of the Euler equations for a polytropic gas with inflow boundary conditions determined by an oscillating piston.
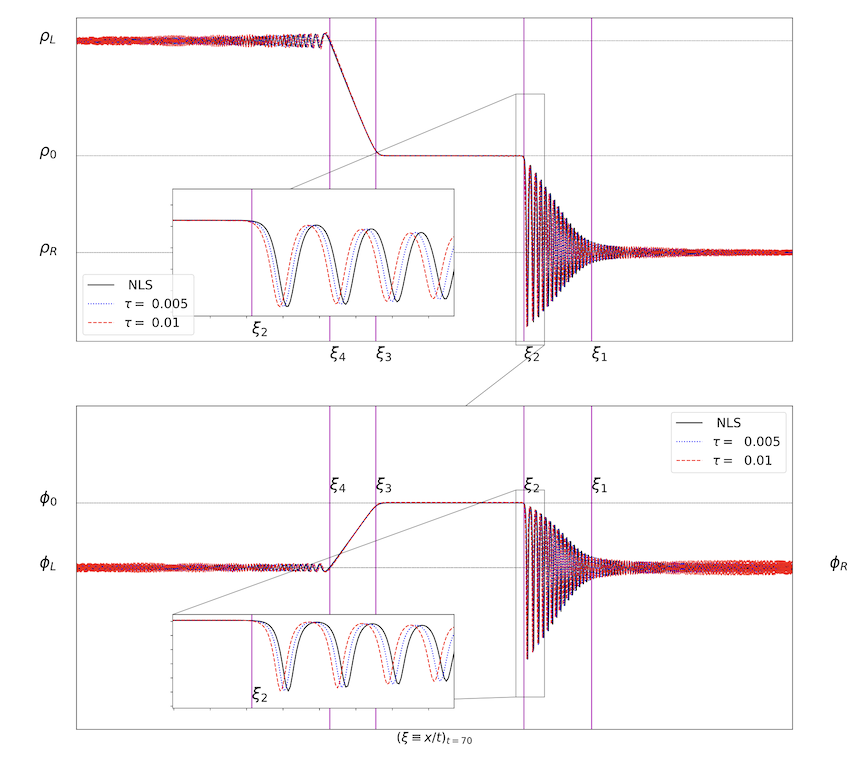
A Hyperbolic Approximation of the Nonlinear Schrödinger Equation
Abhijit Biswas, Laila S. Busaleh, David I. Ketcheson, Carlos Muñoz-Moncayo, Manvendra Rajvanshi
Studies in Applied Mathematics 2025
We study a first-order hyperbolic approximation of the nonlinear Schr\"odinger (NLS) equation. We show that the system is strictly hyperbolic and possesses a modified Hamiltonian structure, along with at least three conserved quantities that approximate those of NLS. We provide families of explicit standing-wave solutions to the hyperbolic system, which are shown to converge uniformly to ground-state solutions of NLS in the relaxation limit. The system is formally equivalent to NLS in the relaxation limit, and we develop asymptotic preserving discretizations that tend to a consistent discretization of NLS in that limit, while also conserving mass. Examples for both the focusing and defocusing regimes demonstrate that the numerical discretization provides an accurate approximation of the NLS solution.
A Hyperbolic Approximation of the Nonlinear Schrödinger Equation
Abhijit Biswas, Laila S. Busaleh, David I. Ketcheson, Carlos Muñoz-Moncayo, Manvendra Rajvanshi
Studies in Applied Mathematics 2025
We study a first-order hyperbolic approximation of the nonlinear Schr\"odinger (NLS) equation. We show that the system is strictly hyperbolic and possesses a modified Hamiltonian structure, along with at least three conserved quantities that approximate those of NLS. We provide families of explicit standing-wave solutions to the hyperbolic system, which are shown to converge uniformly to ground-state solutions of NLS in the relaxation limit. The system is formally equivalent to NLS in the relaxation limit, and we develop asymptotic preserving discretizations that tend to a consistent discretization of NLS in that limit, while also conserving mass. Examples for both the focusing and defocusing regimes demonstrate that the numerical discretization provides an accurate approximation of the NLS solution.
2023
Comparative Study of Iterative Riemann Solvers for the Shallow Water and Euler Equations
Carlos Muñoz-Moncayo#, David I. Ketcheson, Manuel Quezada de Luna (# corresponding author)
Communications in Applied Mathematics and Computational Science 2023
We investigate the achievable efficiency of exact solvers for the Riemann problem for two systems of first-order hyperbolic PDEs: the shallow water equations and the Euler equations of compressible gas dynamics. Many approximate solvers have been developed for these systems; exact solution algorithms have received less attention because the computation of the exact solution typically requires an iterative solution of algebraic equations, which can be expensive or unreliable. We investigate a range of iterative algorithms and initial guesses. In addition to existing algorithms, we propose simple new algorithms that are guaranteed to converge and to remain in the range of physically admissible values at all iterations. We apply the existing and new iterative schemes to an ensemble of test Riemann problems. For the shallow water equations, we find that Newton’s method with a simple modification converges quickly and reliably. For the Euler equations we obtain similar results; however, when the required precision is high, a combination of Ostrowski and Newton iterations converges faster. These solvers are slower than standard approximate solvers like Roe and HLLE, but come within a factor of two in speed. We also provide a preliminary comparison of the accuracy of a finite volume discretization using an exact solver versus standard approximate solvers.
Comparative Study of Iterative Riemann Solvers for the Shallow Water and Euler Equations
Carlos Muñoz-Moncayo#, David I. Ketcheson, Manuel Quezada de Luna (# corresponding author)
Communications in Applied Mathematics and Computational Science 2023
We investigate the achievable efficiency of exact solvers for the Riemann problem for two systems of first-order hyperbolic PDEs: the shallow water equations and the Euler equations of compressible gas dynamics. Many approximate solvers have been developed for these systems; exact solution algorithms have received less attention because the computation of the exact solution typically requires an iterative solution of algebraic equations, which can be expensive or unreliable. We investigate a range of iterative algorithms and initial guesses. In addition to existing algorithms, we propose simple new algorithms that are guaranteed to converge and to remain in the range of physically admissible values at all iterations. We apply the existing and new iterative schemes to an ensemble of test Riemann problems. For the shallow water equations, we find that Newton’s method with a simple modification converges quickly and reliably. For the Euler equations we obtain similar results; however, when the required precision is high, a combination of Ostrowski and Newton iterations converges faster. These solvers are slower than standard approximate solvers like Roe and HLLE, but come within a factor of two in speed. We also provide a preliminary comparison of the accuracy of a finite volume discretization using an exact solver versus standard approximate solvers.
Asymptotic Behaviour of Infinitely Many Solutions for the Finite Case of a Nonlinear Schrödinger Equation with Critical Frequency
Juan Mayorga-Zambrano#, Leonardo Medina-Espinosa, Carlos Muñoz-Moncayo (# corresponding author)
Differential Equations and Dynamical Systems 2023
We consider an N-dimensional nonlinear Schrödinger equation $(P_{\varepsilon})$ with a positive Planck constant $\varepsilon>0$ and power nonlinearity $p>1$. We consider the finite case and critical frequency as described by Byeon and Wang, i.e., the continuous non-negative potential's zero level set is a singleton, around which it decays like a homogeneous positive function. In the limit $\varepsilon \to 0$, we denote the semiclassical limit problem by $(P_{\text{lim}})$. By a Ljusternik-Schnirelman scheme we get an infinite number of solutions for $(P_{\varepsilon})$ and $(P_{\text{lim}})$, $v_{k,\varepsilon}$ and $w_k$, respectively. We prove, up to a scaling, that (a) $v_{k,\varepsilon}$ subconverges to $w_k$ pointwise and in Sobolev-like norm, (b) the energy of $v_{k,\varepsilon}$ converges to that of $w_k$, and (c) $v_{k,\varepsilon}$ exponentially decays out of the zero level set of the potential.
Asymptotic Behaviour of Infinitely Many Solutions for the Finite Case of a Nonlinear Schrödinger Equation with Critical Frequency
Juan Mayorga-Zambrano#, Leonardo Medina-Espinosa, Carlos Muñoz-Moncayo (# corresponding author)
Differential Equations and Dynamical Systems 2023
We consider an N-dimensional nonlinear Schrödinger equation $(P_{\varepsilon})$ with a positive Planck constant $\varepsilon>0$ and power nonlinearity $p>1$. We consider the finite case and critical frequency as described by Byeon and Wang, i.e., the continuous non-negative potential's zero level set is a singleton, around which it decays like a homogeneous positive function. In the limit $\varepsilon \to 0$, we denote the semiclassical limit problem by $(P_{\text{lim}})$. By a Ljusternik-Schnirelman scheme we get an infinite number of solutions for $(P_{\varepsilon})$ and $(P_{\text{lim}})$, $v_{k,\varepsilon}$ and $w_k$, respectively. We prove, up to a scaling, that (a) $v_{k,\varepsilon}$ subconverges to $w_k$ pointwise and in Sobolev-like norm, (b) the energy of $v_{k,\varepsilon}$ converges to that of $w_k$, and (c) $v_{k,\varepsilon}$ exponentially decays out of the zero level set of the potential.
2021
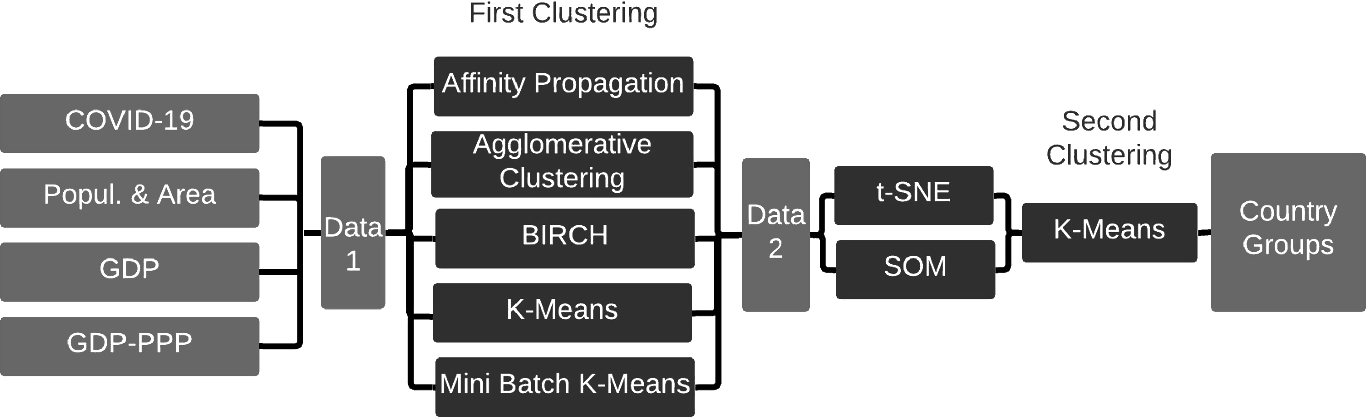
Identifying Similar Groups of Countries According to the Impact of Corona Virus (COVID-19) by a Two-Layer Clustering Method
Juan Riofrío#, Carlos Muñoz-Moncayo, Isidro R Amaro, Israel Pineda (# corresponding author)
Artificial Intelligence, Computer and Software Engineering Advances 2021
This paper presents a new clustering algorithm to identify groups of countries. First, a layer of several clustering methods is applied to the original dataset. Then, after performing dimensionality reduction techniques like t-SNE or SOM on the resulting data, a second clustering layer (K-Means) is applied to identify the final clusters. This method is applied to a dataset from 163 countries, considering the following variables population, area, Gross Domestic Product (GDP), Gross Domestic Product adjusted for Purchase Power Parity (GDP-PPP), and COVID-19 related data (Confirmed, Recovered, and Deaths). The implementation with SOM dimensionality reduction outperformed the one with t-SNE for the considered dataset. We expect that using this information, countries can have an insight on which measures against COVID-19 replicate or avoid, based on the results in countries from the same cluster.
Identifying Similar Groups of Countries According to the Impact of Corona Virus (COVID-19) by a Two-Layer Clustering Method
Juan Riofrío#, Carlos Muñoz-Moncayo, Isidro R Amaro, Israel Pineda (# corresponding author)
Artificial Intelligence, Computer and Software Engineering Advances 2021
This paper presents a new clustering algorithm to identify groups of countries. First, a layer of several clustering methods is applied to the original dataset. Then, after performing dimensionality reduction techniques like t-SNE or SOM on the resulting data, a second clustering layer (K-Means) is applied to identify the final clusters. This method is applied to a dataset from 163 countries, considering the following variables population, area, Gross Domestic Product (GDP), Gross Domestic Product adjusted for Purchase Power Parity (GDP-PPP), and COVID-19 related data (Confirmed, Recovered, and Deaths). The implementation with SOM dimensionality reduction outperformed the one with t-SNE for the considered dataset. We expect that using this information, countries can have an insight on which measures against COVID-19 replicate or avoid, based on the results in countries from the same cluster.